As part of my district job in finding interesting practices going on in classrooms, I came across some your designers in Pam’s class.
Pam is working on her PhD in engaging elementary students in Math. She believes that by activating the affective parts of students’ learning personality, we can engage students’ cognition of Math.
When I went to visit Pam’s class one morning, the students were working on a Math project in Shape and Space that was addressing all the regular curriculum goals. Their task was to think of a possible building and a problem that building solved. Here are some of the ideas students had: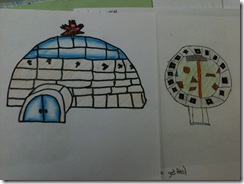
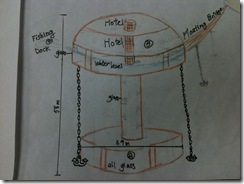
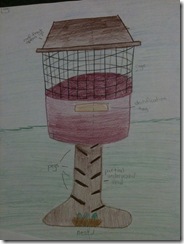
- A boy came up with an igloo design (right) for a restaurant franchise he created. The top part of the dome was glass to let in natural daylight, and at night it was augmented by rainbow lights.
- One girl offered a house on a bridge because it gave privacy. The house was situated on a cliff and bridge could be reeled in. The house was octagonal so that each room had its own section.
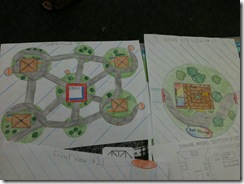
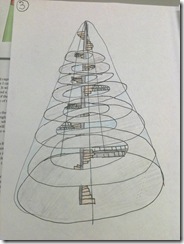
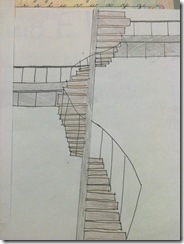
- Another girl offered a spiral staircase design (below) that went through the centre of an art gallery. There were branches that extended off the staircase to access each floor which housed a different artist.
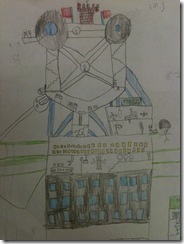
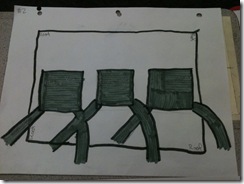
- One boy’s idea was to have a gas station with a series of ramps (below). The ramps would maximize the amount of pumps you could have in a small area. Some of the overhead ramps could be used for a quick oil change.
In their write-ups, students talked about use of shape, symmetry, function, and design.
I asked the students, if they did not have any ideas of their own, to design me an projector cart that did not move until I wanted it to (because my Smartboard frustratingly goes out of alignment too often). In a matter of minutes, Pam’s students had a number of options: velcro and duct tape fasteners, wheel covers, retractable wheels, arms that came out to stabilize the cart when not in motion, and wheels that flipped onto their sides so they didn’t roll but fastened to the floor. We talked about wheels that weren’t round. One girl had in idea to put only two wheels near the bottom, but off to the side so that the cart could be moved like a wheelbarrow (I actually might try this one).
I was blown away! (Did I mention that these students were in grade 4 and 5?) The more they talked, the more they fed off each other’s ideas. Their ideas became more refined but somehow still expansive. One of the reasons these students had so many great ideas was that Pam had inspired them with the work of Thomas Heatherwick. He is a contemporary English designer who design things from hand bags to cafes and hospitals. His buildings look like sculptures. Pam showed her students pictures and videos of Heatherwick’s work to engage that affective and imaginative parts of her students’ brains. They saw the need for the bridges or the buildings, but they were also moved by the beauty and cleverness of his design work.
It is this connection to the affective and imagination that is a large part of Pam’s work with her PhD studies and her investigation of Kieran Egan’s Imaginative Education. She deftly uses Heatherwick’s work to construct a narrative, and the students create personal connections with that story. In turn, their personal connections help them to engage with, for example, Shape and Space concepts in Math. The students see the need for such concepts, and then can apply their imagination to these concepts by using rich tasks, like Pam’s design challenge.
(This post will eventually be part of the district’s public site, but we wanted to share the designs with the families in Pam’s class now).